Alchemy was not merely an attempt to find the Philosopher's Stone or turn base metal into gold. It was a pursuit of uncovering ancient lost wisdom and the search for patterns of order that drive the cosmos. The desire to uncover a "divine symmetry" underlies both ancient and modern pursuits of wisdom.

Sir Isaac Newton was the inventor of calculus and author of Principia Mathematica. He discovered the laws of motion and universal gravitation. He is considered one of the most influential scientists in history. Yet Keynes said of him "Newton was not the first of the age of reason. He was the last of the magicians." That is because Newton's primary passion turns out to be Alchemy.

Squirrel Catcher

At the top of challenging mountain bike runs, trail designers will create a "Squirrel Catcher" feature that indicates the level of difficulty ahead. If the Squirrel Catcher feature seems too difficult at the very top, it serves as warning not to head down the trail. The Comprisation exercise in the beginning of this article may seem to serve a similar purpose. My original intent of the article, though, was to share about Comprisation — a comprehensive approach to combining elements that otherwise result in blind alleys and dead ends. It's why certain truths remain hidden as brilliant minds pass by. I didn't really know anything about Alchemy when I started, but you will soon see where that leads. If you came only for an exploration of Alchemy, you can skim through the simple math down to Searching for Symmetry. If you only want to learn this new finite math technique, you can bail out when I reveal, "This is Where Things Get Weird."

Chaos at the Clubhouse?

We are going to pause the history lesson here and traverse a modern challenge. I was developing a Statistical Process Control system for a major food manufacturer in the 90s. They also consulted with John, a statistics professor from one of the local colleges. One day he came to me with a problem: A Golf Tournament had 32 players, grouped in the standard foursomes. With all players participating in each round, how many unique rounds could they schedule if no golfer ever played with another player twice?

John showed me a letter from a gentleman who had purchased his statistics textbook and was struggling with the problem:

"I've talked to mathematicians, physicists, etc. in my line of work (programming)...I've checked libraries to no avail. They all give me the formula for factorializing, but not the method of generating the combinations. I've tried hundreds of methods, but nothing seems to work. Needless to say, I am very frustrated."

One of my favorite courses at UCLA was Finite Mathematics. Essentially the field involves taking a finite set of elements and finding ways it could be rearranged. The study also forms the basis for understanding odds and probabilistic independence. John assured me there was something about this particular challenge that defied its seeming simplicity. The programmer also sent him pages and pages of attempts at a tournament schedule, but unwanted pairings always snuck into the data. Puzzling...

A textbook simplification of the problem would start by asking, how many arrangements of 4 players could you pull from a pool of 32?

There are a few things—restrictions—already built into the framing of this question: If we were dealing with sets of 26 letters, and making 4 letter words, it might be OK to repeat the same element two or more times. Like the repeated "O" in "DOOR" would be valid. And the order within the set would also matter; "ODOR" would be a different, valid result. So the number of possibilities would be 26x26x26x26 because for each position in the set (the word) there are the full 26 letters as choices. We can make our 32 golfers similar to this example by representing them with 26 capital letters and numerals 1-6. So the set of all golfers distilled to 32 unique characters is ABCDEFGHIJKLMNOPQRSTUVWXYZ123456. Not too bad so far.

Mac Plus vs the Mainframe

I shared my after-work challenge with my friend, Tom, and outlined my thoughts on minimizing the problem space. He laughed and said I was taking that approach because I had a little 8 MHz processor; he was currently working on a mainframe, sorting out the S&L banking scandal. He was sure he could quickly write a program to solve this. He said his plan was to 1) Enumerate all possible player strings. 2) Take a second pass to eliminate any that had repeated characters. 3) Take another pass to check for unique groupings of four. 4) Continue eliminating non-valid matchups.

Essentially he was planning to brute force the equivalent of a Sieve of Eratosthenes for the tournament. (I discuss the Sieve a bit more in The Numbers: Part Three)

Tom wrote the program during a break and launched it on the Bank's Mainframe—Big Iron to handle a big task. I'm not sure how long it was running before he got worried, but Tom executed a diagnostic on the predicted time to finish: 960 billion billion years! Realizing his program was going to consume mainframe resources far longer than he could keep his job, he aborted it.

Ways to re-arrange a set of elements:

• Enumeration
  
• Random
  
• Permutation
  
• Combination
  
• Comprisation
  

Enumeration

Technically, enumeration is really "Permutation with Replacement". But I use the term "Enumeration" when treating all the elements in the set like the numerals of our base 10 counting system. Here 32 unique characters result in a "base 32 string, 32 characters long." For example:
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAC
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAD
etc.
Or 32³² enumerations. Or 1,461,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 mainframe-choking instances that all need checking for duplicates.

Random

After programmers try and then choke on brute force enumeration, they resort to asking the computer to make random assignments, and then filter, according to the restrictions afterward. All this is to avoid studying the problem space and understanding its underlying order.

To demonstrate this for you, I just wrote a quick program to randomly assign foursomes with no replacement. Just 10 rounds and then did a visual scan for players that repeated.

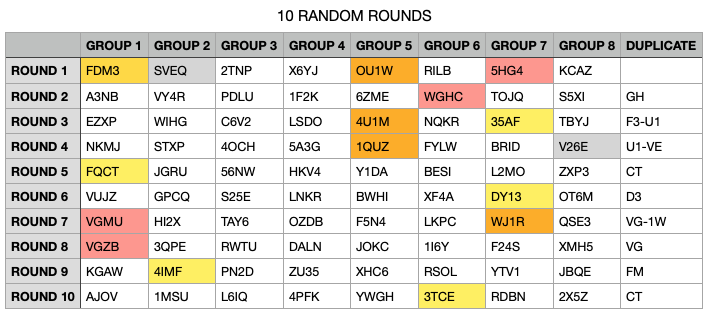
Every round has a conflict with one or more other rounds. I stopped counting.
Random does not work. At all.

Re-scale and Review

Something I frequently do is model a problem at a smaller, but meaningful scale. In this essay, we are going to do that to conserve space and time. Before, we used a single letter (or digit) to represent each player. Now, we will represent each foursome with a single letter, and switch the groupings to two. This would be the equivalent of a tennis singles round-robin with 8 total players. It should have a comparable dynamic, but with only eight total elements to work with:
ABCDEFGH.

We are going to take a brief detour to introduce the "Factorial" notation used in Finite Mathematics, as it will make things easier.

This is pronounced "n factorial" or "n bang!" (which is more fun). "n" represents a positive integer and in our case 8! is shorthand for 8x7x6x5x4x3x2x1. It's a really useful notation for representing how many ways elements in a set can be arranged.

Permutation

If we treat our new limited set of 8 characters as an enumeration (or permutation with replacement), we have 8⁸ or 16,777,216 possibilities.
If we don't allow replacement, the possibilities drop to 8! (or 40,320). That's a lot fewer! The full formula for calculating the number of available permutations is below:

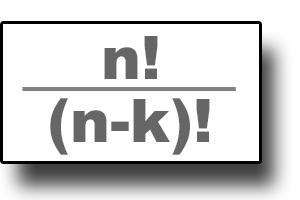
The "n" is still the number of elements, and the full formula introduces "k" which represents how many of the total elements you are going to select at a time. In my example with 8 elements taken all at the same time, "n" = 8 and "k" = 8 so (n-k) = 0. A seeming oddity of factorials is 0! = 1, the same as 1! = 1. Justification (aside from convention, and it works) is the number of ways to arrange a set with only 1 element is 1, and the number of ways to arrange an empty set is also 1. So 8!/0! is 8!/1, or just 8! as I pointed out. To use the formula more productively, we could ask, how many permutations are there from a set of 8 taken 2 at a time?

8!/(8-2)! = 8!/6!
which simplified is just 8x7 (or 56) because we can cancel like terms:

Here is an easier, less mathy way, to think of this: Eight elements taken two at a time is just 8x7. Eight elements taken three at a time is just 8x7x6. See the simple pattern?

What's happening with the permutations above is an arrangement of "A" with every remaining letter, then "B" matched to every other letter, etc. So you get 7 matchups from each letter, eight times. But you are also getting "AB" and then "BA." In our "every player only plays everyone else once" restriction, just changing the order counts as an invalid duplicate. If order doesn't create uniqueness then our restriction leads to "Combinations" and an addition to the formula.

Combination

The formula for Combinations has an additional k! in the denominator, which makes the total smaller. That makes sense as adding an additional restriction should reduce the outcome.

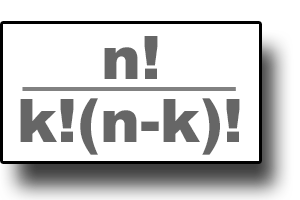
Since k is 2 (at a time) and 2! is 2x1 or just 2, the combination restriction just cuts the 56 permutations in half to 28. So is that the answer? Are we done?

NOPE

The original scenario is not limited to how many unique combinations of 2, it also involves the whole group. If we try combinations of "8 elements taken 8 at a time" that answer is just 1. So now we are stuck in the same position as the guy who wrote to the professor.

We find our problem:

• Is NOT an Enumeration
  
• Is NOT a Permutation
  
• IS NOT a Combination
  

Comprisation

"Comprisation" is a term I coined for this specific scenario, which combines the restrictions of a Combination, but across all subsets AT THE SAME TIME. Since "The Whole Comprises the Sum of its Parts" the term seemed appropriate.

We are also not going to just predict how many valid rounds we could possibly create, we are going to actually populate them. Let's start with a template:

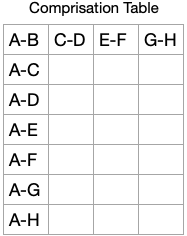
That's a pretty good start. The first round is defined. And we can see how many rounds are possible with our "Comprisation" restriction: Seven. Once "A" has combined with each of the other letters, we are done. A further row in the table would guarantee a duplicate. Can we fill in the rest?

Four rows completed. Let's check our work:

• Check 1. Each Row: Every Letter Used.
  
• Check 2. Each Row: No Duplicate Letters.
  
• Check 3. Each Subgroup of 2 is Unique to the Table.
  
• Everything is valid so far...
  

It should be pretty easy to fill in the last nine cells.
Take a moment and complete the remaining 3 rows!
(Hint: I would not have dragged you through all this if this tiny exercise didn't make an important and fundamental point.)

.

.

.

Here's a completed table that passes the first two checks...

Oh, wait!

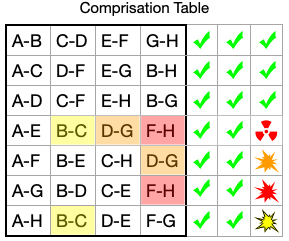
Three of the cells from the added rows have a pairing already used!
Here is the kicker...
You could start rearranging and rearranging, but duplicates are going to keep popping up. It will become very frustrating. So does this mean there are only four possible rounds? No, there is a solution for all seven possibilities. The solution requires the equivalent of a "paradigm shift." But you may find the technique surprising.

Searching for Symmetry

I created this technique many years ago, working with pencil and paper.

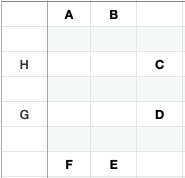
The method is to switch away from table representations, to a graphic one. Draw connections and then look for patterns of symmetry.

Here are the first 4 rows of the table, now represented graphically:

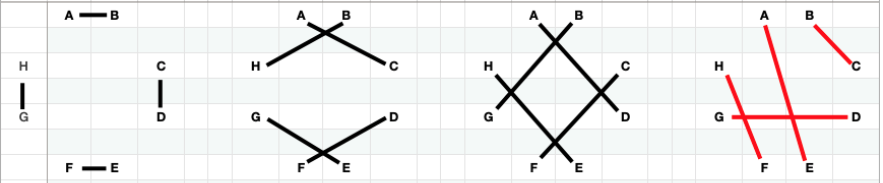
What is notable is that the fourth arrangement does not have the symmetry of the first three. The stated problem says nothing about a graphical symmetry requirement, yet here it is. What the fourth arrangement does is poison any further comprisations so the full set cannot be achieved. If you did the exercise to fill in the table you will have experienced that first hand. Essentially, the fourth arrangement is a valid theory in our problem space, but in context, it creates a dead end.

Let's fix it.

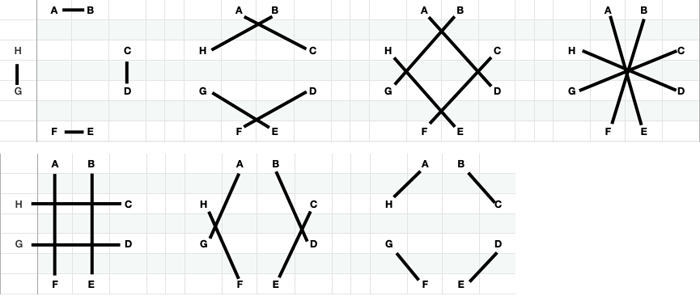
Once the non-symmetrical 4th group is replaced by the radially symmetrical one, the remaining three are simple rotations of the first three! That's all seven. That's the solution.
(I will leave it to the highly motivated reader to extend a similar technique to the ¹golf scenario with foursomes.)

The important takeaway is that there exist "Poison Patterns," that while valid themselves, prevent completion of the full solution. A way to detect and avoid them is to analyze the solution geometrically, searching for patterns of symmetry.

This is Where Things Get Weird

I try and create meaningful information in the banners of these essays. This one is not an exception.

To keep the eventual "comprisation" solution from being too obvious, I decided to switch the eight letters (ABCDEFGH) with symbols of some sort. Looking through the Unicode glyphs I thought about astrological symbols, but it's a set of 12. Planets have symbols too, but which ones? I remembered from language studies that the seven days of the week are normally named for gods that represent planets, or more correctly "the wanderers." Sun ⊙, Moon ☽, and 5 planets ♂☿ ♃ ♀ ♄ that have been noticed since antiquity. To match all 8 of my letters I added the symbol for Earth ⊕.

Since I was illustrating my 4 patterns I came across the classic Aristotelian Elements: Earth, Water, Air, Fire. It turns out these are core to the pursuit of Alchemy, especially the relationship between them.

It's interesting that the classic symbols for the classic elements above are also geometric rotations.

I had hoped to find some Issac Newton sentence that mentioned a quest for a hidden "divine symmetry." I was not successful searching the quote libraries, but instead found a massive, obscure trove of his unpublished "Hermetic" writings—a million plus words!

Today we find it paradoxical that an esteemed scientist would devote much of his thought to a seemingly silly endeavor. Alchemy was outlawed in England at the time Newton was experimenting, so this part of his life was secretive. Concerns about magically expanding the gold supply would be of national concern, and charlatans took advantage of those thinking it was possible. But Alchemy, for serious practitioners, was the state of science at that time. Gold, Silver, Copper, Mercury, Lead, Sulphur; all staples of the Alchemists lab, are recognised today in the Periodic Table of Elements. By re-arranging various atomic elements, alchemists were hoping to gain insight into the inner workings of "God's creation." Math describing Universal Gravitation (F = G(m₁m₂)/R²) would be a fortunate byproduct.

Newton's subjects and descriptions in these "Hermetic" documents are a far cry from my experience with reading the "Laws of Motion." His private texts are full of the exact same planetary symbols in the header graphic ⊙ ☽ ♂☿ ♃ ♀ ♄, and with the continued arrangement of the 4 Elements 🜃 🜄 🜁 🜂 , all in the pursuit of a "Philosopher's Stone."

Newton draw diagrams with similar rotational arrangements, but based on seven nodes instead of my eight. I found it uncanny that "Newton the Scientist," and "Newton the Alchemist" also used combinatorial geometry to explore the same problem space: The Boundaries of Objectivity. And it turns out Newton was not the only one...

PART TWO »