Previously on The Numbers...

In Part One we touched on Number Sequences, discovered a simple formula to test a Fibonacci number, and fixed upon the Prime Numbers.

In Part Two we continued exploring Prime Numbers: Their diminishing, but infinite, distribution; and their critical role in digital security. Most importantly we introduced the controversy of whether Prime Numbers were randomly or predictably distributed.

"The prime numbers belong to the most arbitrary and ornery objects studied by mathematicians: they grow like weeds among the natural numbers, seeming to obey no other law than that of chance, and nobody can predict where the next one will sprout. The second fact is even more astonishing: The prime numbers exhibit stunning regularity, there are laws governing their behaviour, and they obey these laws with almost military precision."
—Don Zagier, 1975

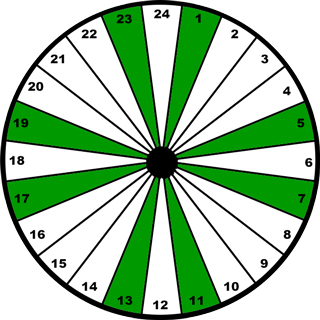
Analyzing Grant's 24 Sided Wheel

I created a simplified version of Grant's Wheel to study the salient points. The first thing to notice is the very apparent symmetry in the arrangement of the Prime Numbers. Laid out in a string, that relationship can be missed. Another observation is that the colored primes can be paired: 1-23, 5-19, 7-17, 11-13; and each pair equals 24, which is also the total slices on the wheel! This really begins to make the case for a pattern rather than just a random occurrence of the Primes.

How a Prime Wheel Works

Grant's wheel turns out to be an example of a "Prime Wheel" or "Wheel Sieve" with 24 slices. The savvy reader may also note that the visual symmetry may appear as the result of "cheating" since 1 is frequently not considered prime, and 2 and 3 are being skipped. But more investigation into Prime Wheels shows this particular treatment of 1, 2, and 3 is normal.

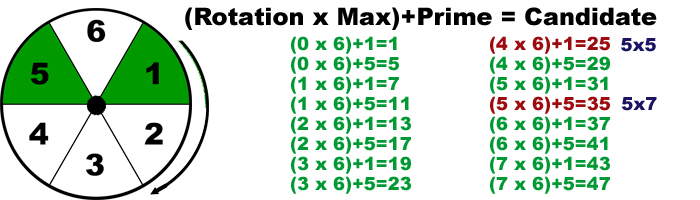
Above is a minimalist Prime Wheel, with only 6 slices and two supplied Primes: 1 and 5. To generate a series of Prime Numbers you start with Rotation = 0 and pick up the Primes already assigned. With each subsequent rotation, you pick up more new primes. We started with only 1 and 5 and ended with 1, (2, 3,) 5, 7, 11, 13, 17, 19, 23...

Size Matters

With a small starting wheel, we will get new good primes right away, but after many rotations, some false primes will appear. These false primes (composites) will have to be filtered on a subsequent validation pass. But it's important that no valid primes are missed with the initial list.

Even Smaller

We could make an even smaller wheel. It has 1 slice and 1 prime: 1. It will produce every single prime. But that's because on each rotation it adds 1 to the sequence, producing all counting numbers - primes and all the rest. If we look at the 6-Slice graphic above we can see the next wheel size up also yields all the prime numbers and some others that need to be filtered. The ratio of good primes to composites, which need filtering, is the key.

Separating Wheat from the Chaff

The most ancient method for removing non-primes from a list comes from the 3rd-century BCE Sieve of Eratosthenes. Essentially the method is to produce a block of all counting numbers, and then eliminate a series of them, according to a sequence rule (e.g. eliminate all numbers divisible by 2). The method proceeds by starting with the smallest prime: 2, eliminates all numbers divisible, and then starts again, eliminating the remaining numbers divisible with the next largest prime. In the end, only prime numbers are left over.

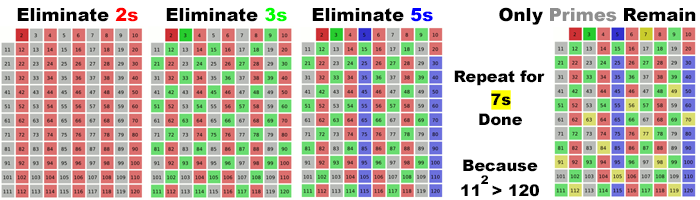
This method filters all the non-primes, but is a lot of work. One property stands out, however. By testing from the smallest prime upward, we don't have to check every number against every other number, or even every prime less than the max of the set. For the number series up to 120, we only have to run the elimination for 2,3,5,7. Why is that?

All non-prime numbers are composite (made from multiplying smaller prime numbers together). The smaller the prime is, the more work it can do in sieve elimination. 2 eliminates 1/2 the number series right off the bat! When it's 3's turn, it starts checking at 3*3 = 9. It doesn't have to check smaller multiples, like 6, because 2 already took care of 2*3 = 6. It can be thought of as the Square Rule. The next prime starts at its own square since combinations with smaller primes have already been eliminated. 5 starts at 25 (5*5) and 7 starts at 49. 11 never gets started because 11*11 = 121 and this series ends at 120.

A more compact, mathy way, would be to say the primes used are less than the square root of the max number in the series. √120 = 10.95. So checking primes in this series ends before 11.

Can this be Simpler? Yes.

The first thing I see is that the Sieve requires I generate all counting numbers to the requested max, and then I have to immediately go back and eliminate every other one. What if I only generated every other number to begin with, instead of having to eliminate them later? It would save 50% of the work.

That's exactly what the 6-Slice wheel is doing. It's skipping multiples of 2, and skipping multiples of 3 also! So instead of generating 120 numbers, 81 of which have to be eliminated, it generates 40 candidate numbers and only need eliminate 11. Massive time savings!

Skipping More Multiples

The diagram shows that multiples of 5 account for the majority of composites generated. 5x5, 5x7, 5x11, 5x13... No multiples of 2 or 3 were generated. Can we just pull 5 off the wheel?

We can check what would happen if 5 were removed by looking at the calculations above and eliminating the ones with "+5." The resulting candidates would be 1, 7, 13, 19, 25... Wait, what? Eliminating 5 from the wheel didn't prevent composite 25 = (4x6)+1 from being generated, but we also missed real primes along the way (11, 17, 23). We can't just pull 5 off the wheel like we did with 2 and 3.

Grant Adds More Primes

The Grant Wheel has 24 slices, like hours in a day, with a promising visual symmetry. Is the secret to prime generation a 60-Slice wheel, matching the minutes in an hour? 360 degrees in a circle? Are we chasing a divine symmetry? How does the 24-Slice Grant Wheel compare to the 6-Slice wheel?

Honestly Surprised

Compare the table data between the 6-Slice and 24-Slice wheels. The results are EXACTLY the same! They match 100% with primes (green) and composites (red) generated, despite a 400% increase in primes and slices of the Grant Wheel. Not just the count, but the same exact ones. And the prime number 5 still accounts for over 60% of the unwanted composites. I never noticed this until making the graphic. Also note that for the value in each row, the column to the right is always 30 higher. More symmetry.

The Secret to Fewer Composites

There is a secret to even fewer composites without missing any of the primes. It is a bigger wheel with more skipped primes. But there are rules, (to be revealed in part four).

Some quick observations: This 30-Slice wheel eliminates the 5-based composites. The same 7-based composites are still left, but it cuts to total non-primes from 11 down to just 4. Why does a 30-Slice wheel outperform Grant's 24? We've stopped generating all the composites based on 2, 3, and 5. What would it take to get rid of the 7-based composites too?

Are we almost at a perfect solution?

PART FOUR »