The Numbers PART FOUR
March, 2024

Previously on The Numbers...
In Part One we touched on Number Sequences and discovered ChatGPT hasn't mastered the topic of Prime Numbers. And that there is a $1 million prize for someone who does.
In Part Two we introduced the Crown Sterling controversy and a claim that prime numbers follow a pattern, and the pattern unravels the current basis for digital security. We are also introduced to the Mysterious Grant Wheel.
In Part Three we analyzed the Grant Wheel, discovering it's a suboptimal 24-Slice wheel for generating prime numbers. A 6-Slice wheel performs the same as the 24-Slice wheel. A 30-Slice wheel outperforms both.
Cracking the Code
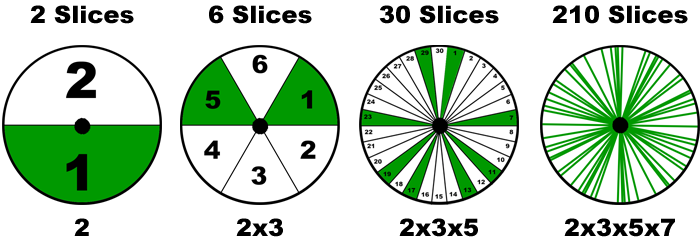
We briefly covered the fact that a 1-Slice wheel would just output every single number. A 2-Slice wheel would eliminate even numbers, thereby cutting the filtering work in half. 6 slices, shown above, eliminate multiples of 2 and 3. To eliminate composites of 2, 3, AND 5, we need to create a prime wheel with 30 slices (not 24). The magic rule is when eliminating the next larger prime from a wheel, the new total slices needed are the PRODUCT of the primes to be skipped. To skip 2, 3, and 5, you require a wheel with (2x3x5)=30 slices. To remove 2, 3, 5, 7 you need (2x3x5x7)=210 slices.

The graphic above starts the 210 Slice Wheel at Rotation 1. That's because values for Rotation 0 are manually assigned and would take up the entire table. It would appear to be perfect. However, by showing Rotation 1, we can see the 210 wheel still generates composite candidates. It just starts happening later, at the larger values.
Here are a few conclusions so far:
- Prime Wheels output Candidates for Prime Numbers.
- Among the Candidates, valid Prime Wheels will output ALL the prime numbers.
- More non-prime Candidates appear as the values get higher.
- Larger Prime Wheels output fewer non-prime Candidates than smaller wheels.
For the table above, the Green text represents the verified Primes. The Red text highlights candidates that failed the primacy text. Notice the Blue Numbers in the table. They are populated like primes on the wheel, but notice they are not prime themselves (eg 121=11x11). Blue Numbers don't occur on the smaller wheels. They may be the best-kept secret of Prime Wheel creation.
Experimentation, Application, and Experience
My personal investigative procedure is to first think things over, then try things out with pencil and paper. If the direction is still promising, I move to spreadsheets, and finally, I will build an application.
I was at the application stage when I built my first 210-Slice wheel. As user inputs, I could select wheel size and even the starting and ending range. The output would show the validated primes and also the failed (detected as non-prime) candidates and reason. I could save the successfully detected primes in the program and to a file. This means I could start with a small Prime Wheel (6), and use the verified prime numbers output to populate the next larger Wheel (30 then 210 then...). Because the definition of a Prime means it is not a composite of any smaller prime, it is critical that the list is perfect as it is being created.
Primes Published to a Million
I was fortunate to find a verified list of primes from 1 to 1 million. This was important to be sure my wheel creation method, my application, and my filtering algorithm were without error. There are 78,498 primes in the list and they can be viewed in a simple text editor on 78,498 lines. If you create your own list of a million you can at least check that the line counts match. Which, for the 210-Slice Wheel, they did not. Primes were missing. This is how I discovered what I'm calling the "Blue Numbers." And how it relates back to the Grant Wheel.
If we look at an array of the values for the 30-Slice wheel it is [1,7,11,13,17,19,23,29] -- Primes less than 30; skipping 2, 3, 5.
If we look at an array of primes less than 210; (skipping 2,3,5,7) it is [1,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199]
Presented as an array, the Grant-like symmetry is not apparent. For the 30-Slice Wheel, we can pair them all up: 1+29=30, 7+23=30, 11+19=30, 13+17=30.
For the 210 array of primes, 11+199=210, but 1 is an orphan. There is no matching prime. So if subtract 210-1=209, we have our first Blue Number. There are five of them for the 210-Slice Wheel. Their inclusion makes 210 a valid Prime Wheel. It will now produce ALL the Prime Numbers, like the smaller wheels, and will also generate fewer non-prime candidates.
These are the Rules
Now we know the rules for creating bigger and bigger Prime Wheels:
- The number of slices required by a wheel is the product of the primes being skipped.
eg. 2x3=6, 2x3x5=30, 2x3x5x7=210, 2x3x5x7x11=2310. - Every value on a wheel must have a complement that sums to the max slices.
- Any orphaned prime must be matched with the proper composite (Blue Number).
- Primes populating a larger wheel can be first generated by a smaller wheel.
Relative Performance
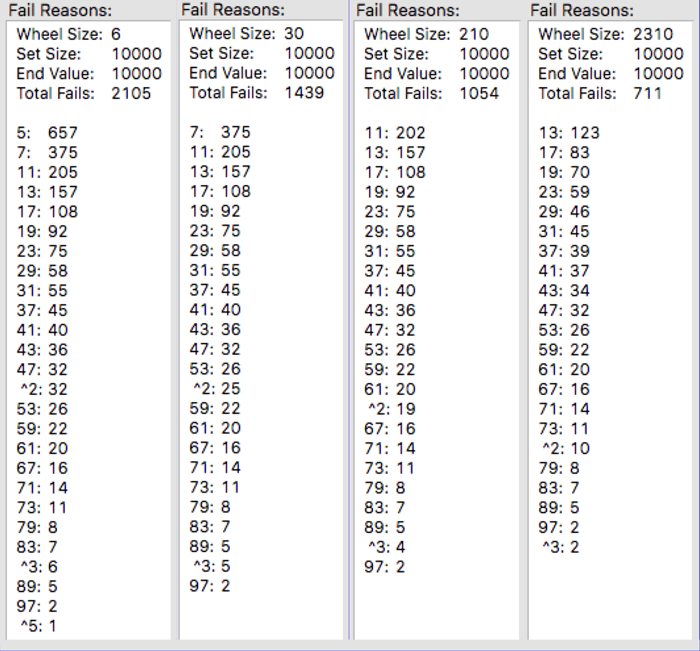
The results above involve successive Wheel sizes each generating the list of primes from 1 to 10,000. The term "Fail" refers to a Candidate number the wheel generated, which turned out to be a composite number and not a prime. As the wheel size increases, the number of fails goes down. That's the good news.
The bad news is what it would take to generate the perfect list of 10,000 with no "fails." From the 2310-Wheel we can see we would need to skip more primes, specifically those under 97. What size wheel would that take?
We would have to skip 2,3,5,7,11,13,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97. Yikes. Actually multiplying all those numbers together blows up my calculator and spreadsheet and you end up with scientific notation which rarely gives the same impression. Let's be MUCH more modest and stop at 41. A wheel that skipped Primes through 41 would require over 300 TRILLION slices. We would need to have already solved the list of Primes from 1 to 300 trillion. And skipping 41 still would not give a clean list of 1-10,000 candidates. It turns out none of these bigger wheels generate a clean list of prime candidates after the first rotation. So, in the next section we need to address: