Previously on The Numbers...

In Part Four we uncovered the rules for creating larger and larger Prime Wheels. Larger Wheels create fewer non-prime Candidates, but they will always create some. This is a disappointing discovery.

It's Worse

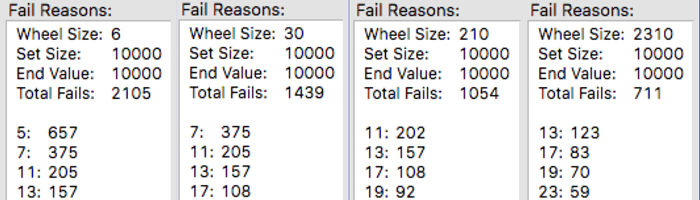
To generate fewer non-prime candidates from the output, we have to build a wheel that skips over a prime factor. For a Wheel Size of 210, the prime number 11 accounts for 2% of the "fails" (composite candidates), which is the highest percentage. To remove 11, we "merely" build a new, larger wheel. But it will be Wheel Size 2310, eleven times larger! Removing that one prime means adding about 300 more known primes to the bigger wheel. It gets much worse as the wheels get larger. But...

Performance Sweet Spot

I built the next two larger size wheels anyway. 510510 is a beast and requires already knowing the primes over half a million. In my application, it seems slow to create, as all of the Blue Numbers have to be calculated too. However, it was a worthwhile exercise as it revealed a sweet spot.

These speeds, in seconds, are relative to my software and system. They also represent the time required to generate all of the Candidates and identify which are composites. Since the giant wheel was already configured with half of the primes to 1 million, it might promise to be the fastest. But 2310 is the sweet spot and we don't need to focus on ever-increasing wheel size. We need to focus on detecting non-prime candidates.

From Fibonacci to Fermat

Thinking back to Part One and the discussion of Number Sequences, recall there were basically two challenges:

• 1. Generate a full sequence of items, according to a defined rule.
• 2. Detect if an isolated item would be a valid member of the sequence.

The Fibonacci Sequence is the closest challenge to the Primes in that every subsequent Fibonacci number depends on previous Fibonacci numbers: 1,1,2,3,5,8,13,21,34...
Fibonacci has two properties we WISH we could discover for the Primes: Every new number generated from the previous two will be correct. There are no "Candidates" which require separate validation. And given a larger, isolated number, a formula was discovered to test its "Fibonacci-ness": If n represents a Fibonacci number then either (5n²+4) or (5n²-4) must yield a perfect square.

In 1597, Sir Francis Bacon first published his "Esseyas". Let's use our algorithm to see if n=1597 is a Fibonacci number by checking (5n²+4) :

5(1597²)+4
5(2,550,409)+4
12,752,045+4
12,752,049
√12,752,049 = 3,571.001120134240451 (THE DECIMAL MEANS IT'S NOT A PERFECT SQUARE!)

OK. Let's try (5n²-4) :
12,752,045-4
12,752,041
√12,752,041 = 3,571 (It's Fibonacci!)

Note that we have a definitive Fibonacci answer in at most two steps. And the answer is "YES." There is no list of "Candidates" that require further validation. Isn't there an equivalent formula for testing a Prime?

Fermat's Little Theorem (FLT)

If Fermat solved the Mystery of Primes in 1640, we would not be on this journey, there would be no $1 million prize, and digital security would be different. So we already know it's going to fail. But how close was he?

If "n" represents the number we want to test for Primality, and "a" represents an integer greater than 1 and less than "n", Fermat's test is:
a^n-1 MOD n = 1

(Don't get thrown by "MOD" if you've never used it. It just means divide the number to the left of MOD evenly by the number to the right as many times as you can until there is 0 or a remainder. A simple MOD example: 5 MOD 2 = 1)

The smallest "a" value allowed by Fermat is 2 so let's use that. 13 is one of the lower Fibonacci Numbers. We can test if 13 is also Prime using Fermat's test:
2^13-1 MOD 13 = 1
2¹² MOD 13 = 1
4,096 MOD 13 = 1
1 = 1 (It's Prime!)

OK. Let's try 1597 and see if we have another "Fibonacci Prime." (That's a number both Prime and in the Fibonacci Sequence. There are only 10 of these less than a Billion. Witness the miracle!):
2^1597-1 MOD 1597 = 1
2¹⁵⁹⁶ NOT A NUMBER.
Error description: numeric: range error (overflow)

Here we discover the first main problem with implementing Fermat's Little Theorem (FLT): It checks primes as an exponent. 2¹⁵⁹⁶ is TOO GIANT A NUMBER. It's already 480 digits long! How well would this work for checking primes in the millions? It's already out of control.

The second and most cited issue with FLT is it's vulnerable to confirming "Pseudo Primes" and "Charmichael Numbers." 561 is the smallest Charmichael Number and the FLT will falsely show it and the other Charmichaels as prime (i.e. 3x11x17=561, not a prime number.) It's not reliable.

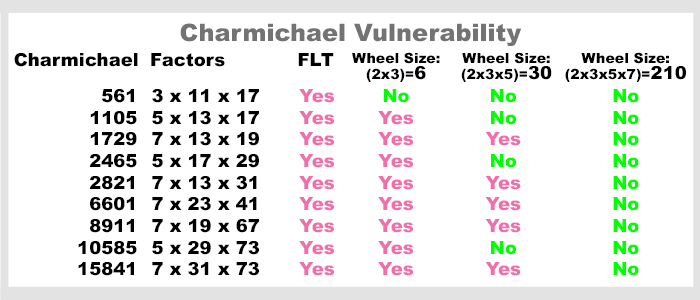
If a Wheel is built to skip a Prime Factor, it will not even generate the pseudo prime as a Candidate. Wheel Size 210 does not generate the first nine Charmichael Numbers. It's a promising direction.

Joking aside, Fermat's Little Theorem is quite an achievement, centuries before calculators and giant cryptographic primes. It is useful for eliminating composites. It might not be perfect when declaring a Prime, but if it says a number isn't prime, it never is. I still don't like using primes as an exponent because it's going the wrong way mathematically. There is a technique, however:
2^1597-1 MOD 1597
2¹⁵⁹⁶ MOD 1597
because 1596 = 399+399+399+399 we can
((2³⁹⁹ MOD 1597)x(2³⁹⁹ MOD 1597)x(2³⁹⁹ MOD 1597)x(2³⁹⁹ MOD 1597)) MOD 1597
((610)x(610)x(610)x(610)) MOD 1597
(138,458,410,000) MOD 1597 = 1 )(It's Prime!)

OK, but Yuck.

Prime wheels also don't create false negatives. If a number is not generated by a wheel, it can't be prime. Here's how we would check 1597 on the simple 30-Wheel. It's the reverse of (Rotation x Max)+Prime = Candidate:
1597/30 = 53 remainder 7
Since 7 is a slice on the 30-Wheel, we know 1597 was a Candidate. DONE.

If You Thought (FLT) was Ugly

The current Standard for prime number generation is Miller-Rabin. It seems to be a mutation of FLT, crafted to avoid Charmichael Numbers. But it continues with giant exponents, MOD math, and several IF/THEN steps. There is an online calculator HERE if you'd like to learn more. The main takeaway, however, is that Miller-Rabin is a Prime Generator, not a Validator, and it's a Probablistic generator. What the algorithm returns is "Probably Prime" and depends on several RANDOM input cycles. The more cycles it runs, the lower the probability it has of returning a False Prime.

In Primality Testing Under Adversarial Conditions, the authors write, "Due to its probabilistic nature, it is well known that a t-trial Miller-Rabin test is only accurate in declaring a given composite number to be composite with probability at least 1-(1/4)^t."

They go further with, "for a number of libraries... we can construct composites that always pass the supplied primality tests."

To me, this is the equivalent of Fermat's vulnerability to Charmichael Numbers, but somehow, because it uses RANDOM NUMBERS there is widespread comfort with its use. This is what Grant was complaining about when he wrote "methods... considered more probabilistic than exact...and if they pass, then they are considered most probably prime."

That Leaves Trial Division

We have several ways to generate better and better prime candidates, but often we need to be 100% certain of the result. Final Validation ultimately relies on the definition of Primality: The number can only be divided by 1 and itself. And that means Trial Division.

CONCLUSION »