Previously on Comprisation...

In Part One I introduced a more sophisticated constraint surrounding the reordering of elements. Since the model requires combinations of several subsets across a superset simultaneously, I named these type of problems "Comprisations." To obscure my problem solution, I changed my example letters to planets in the header graphic. It added an "occult" flair to the image and is actually an example of an occult practice. Bring in an Isaac Newton quote and we are headed down the rabbit hole of Alchemy.

In Part Two I clarified the meaning and method of "Occult" and introduced the "As Above, So Below" model of the Hermetic tradition. I also claimed the European Enlightenment period as the split between Science and Mysticism, with Issac Newton personifying both branches. We followed a brief 2,000 year thought transition, from "changeless atoms" to "elemental symmetries." The fundamental nature of symmetry echoes back to the point learned by the Comprisation exercise.

In Part Three we explored the mapping between Aristotelian Elements and the Platonic Solids. We attempted to use "Metatron's Cube" as a template for the Solids, but found it supported all but the Pentagonal based shape. However, Jonannes Kepler did build a model of the planets, associating orbits and distances with a similar concentric arrangement of the Solids. Kepler later abandoned this model, discovering the planetary orbits were elliptical instead of perfectly round. This became a later inspiration for Newton's work.

An Ironic Side Note

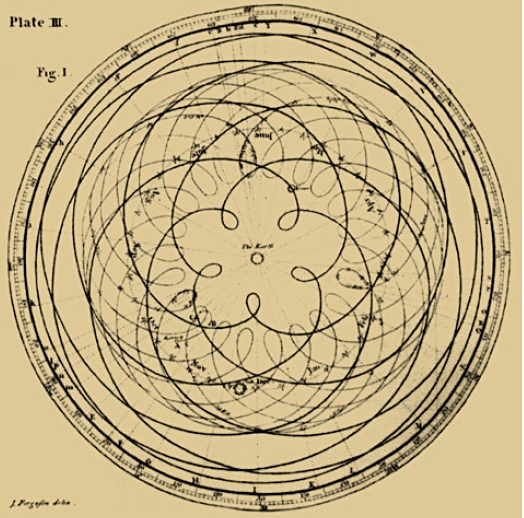
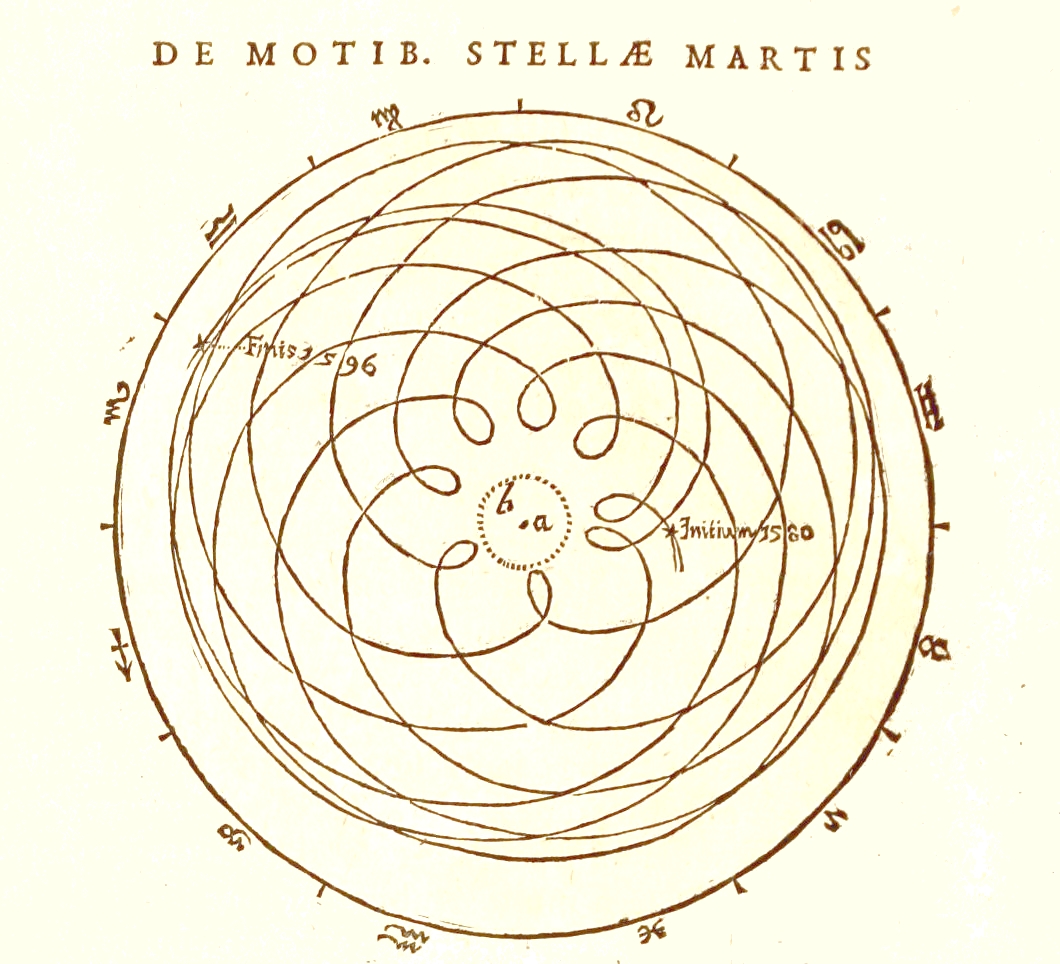
I previously called out that the Metatron's Cube did NOT work to generate the pentagon based dodecahedron. Kepler used the dodecahedron in his model, but didn't claim it came from Metatron. He placed it between Earth and Mars and this seems to me similar to generating the "poison pattern" from my comprisation example. The irony comes from the orbit of VENUS, which every 8 years creates a visual pattern of "the rose" or five pointed star, or a PENTAGRAM. It's almost "perfect," rotating only 1.5 degrees over the eight years, and those studying planetary motion would definitely notice the shape. The illustration below was done by James Ferguson in 1799, but next to it, Kepler made the exact kind of projection for Mars in 1609. Kepler certainly would have known of the Pentagram or rose of Venus.

Standing on the Shoulders of Giants

Newton famously wrote, "If I have seen further, it is by standing on the shoulders of giants."
Johannes Kepler would easily qualify for Newton as one of those Giants. German polymath Gottfried Leibniz, certainly would not. Newton accused Leibnitz of plagiarizing his work on Calculus. But today both men are credited with independently inventing the technique. They were both innovative mathematicians, and they were both Alchemists seeking the Philosopher's Stone.

Leibniz wrote many books, ranging from "A Philosopher's Creed" to "Explanation of Binary Arithmetic." In fact, some consider Leibniz to be the first computer scientist:

"The general idea of a computing machine is nothing but a mechanization of Leibniz's calculus ratiocinator." — Norbert Wiener (1948)

Directly related to our discussion on Comprisation is Leibniz's — "On the Art of Combinations" from 1666. A later edition (1690) includes the illustration below, showing combinations between the "Classic Elements" and "Classic Qualities." In my article The Elements I go over the Classic Elements angle in more detail, so I won't repeat that here.

The topic proposed in "Art of Combinations" was Leibniz's plan to devise a universal alphabet of thought. He termed this "characteristica universalis." These symbols would be visually intuitive for normal people. Yet the full complement of symbols would enable the expression all mathematical, scientific, and metaphysical concepts.

Leibniz theorized a physical mechanism that would process combinations of characteristica universalis symbols and calculate the truth of the arrangement. He named that machine "calculus ratiocinator." Combined, these two would be the hardware and software of universal knowledge. He actually built a less ambitious prototype of the machine, limited to mathematics. It's called the "Stepped Reckoner" and was the first calculator that could perform all four basic arithmetic operations. The primary innovation was the "Leibniz wheel" which was then used in mechanical calculator designs for another 200 years.

If this seems like Leibniz proposed a plan to build the ultimate AGI (Artificial General Intelligence) you would be correct. But he didn't see it as a dominating sentience. In the same way mathematics resolves relationships between numbers, the calculus ratiocinator would establish truth among ideas. Leibniz saw it as a way to amicably settle disputes between individuals or even nations. "...One could always say: let us calculate, and judge correctly through this."

So here we summarize: Leibniz pursued an ultimate source of knowlege, represented by elemental symbols of thought, and processed through a mechanism of intersecting wheels. We might have missed an important ingredient but Wikipedia supplies it:

"Complex thoughts would be represented by combining characters for simpler thoughts. Leibniz saw that the uniqueness of prime factorization suggests a central role for prime numbers in the universal characteristic." —  Wikipedia on Gottfried Wilhelm Leibniz

Leibniz apparently dabbled in Alchemy, but nowhere to the extent that Newton did. He gives a somber warning about the pursuit, which will touch on in my later Doomsday Mechanism article.

In PART FIVE we will revisit Mr. Newton, who built upon Kepler's insights to understand the motion of the planets. We will also explore an alchemical model Newton secretly worked on. A model based not on the 4 sided symmetry of the Classic Elements, or 6 sided symmetry of the "Flower of Life" but rather a more mysterious model with seven axes.

PART FIVE »