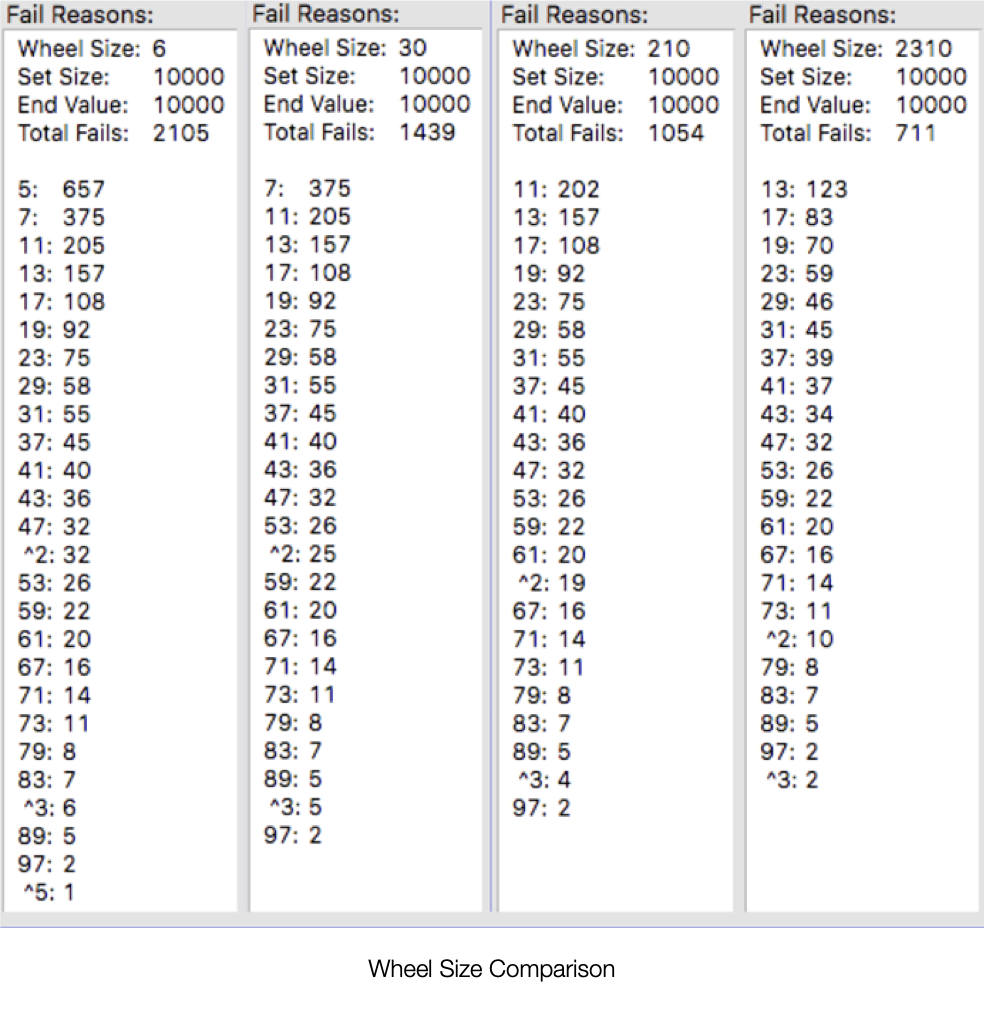
The 2310-slice wheel produces only 1/2 as many Composities as the 30-slice wheel (good), but it requires 77 times more slices (horrific). Creating ever-bigger wheels is not even close to a scalable solution. In the Conclusion of "The Numbers" I assert the only solution would be finding new rules in math that would treat large primes like strings of numerals instead of numbers. Or perhaps building a "Prime Clock" that would somehow filter the Composities so they are never produced.

Contact with the Cosmos

In my article "Pareidolia" I reveal I had a vision for the design of a Prime Clock, months after putting "The Numbers" article to rest. The vision turned out to be the intersecting rings that appear in Carl Sagan's movie "Contact," and also a 17th century woodcut of "Ezekiel's Wheel," and the "Armillary Spheres" invented by Eratosthenes, who also invented the "Sieve of Eratosthenes" (for doing trial division of prime numbers), around the time the Antikythera Mechanism may have also been invented. (All those connections came to light later, gradually over the months, while writing these articles.)

I decided to start my Prime Clock design with the 30-Slice wheel. My attempt would be to create subwheels, or gears, with each of the 8 slice points: 1, 7, 11, 13, 17, 19, 23, 29. Wheels larger than 30 slices are are a bit more efficient, but have WAAAY more slices that would need gears computed for them. Also recall from "The Numbers" that there are composite "Blue Numbers" that occupy some slices when the wheel gets larger than 30. That's was another reason to start with the 30-Slice Wheel.

The next step was chase down what is happening in all the "Fail Reason" composites. What was the minimal prime factor for the "Fail", on which slice, and under which rotation? Write it all down.

After gathering data from a substantial number of rotations it's time to rearrange components of the data into rows and columns of a spreadsheet. There will be a stack of papers with multiple pencil notations, circling each diagram. It's determination, like Jodie Foster on the hood of her car, scanning raw data for some sign of intelligence. I was "on the hood" for about a month.

And then...there it is.

Eureka!

The pattern wasn't quite as obvious as I had initially assumed. It was three layers deep. But it was there, and it was repeating. The repeating numbers exist for each slice and each slice is unique. Arranged on a spreadsheet they unexpectedly form a giant SUDOKO "Golden Matrix." The Golden Matrix drives the "Red Numbers" which in turn drive the "Skip Numbers." I also placed the Golden numbers into a Comprisation template, which revealed the signature symmetry of being a "Complete Solution."

To the skeptical reader this might sound like a non-reproducible ticket to "Kookville." Except I enhanced my previous Prime Wheel application (V2) and I can compare it to the new "Prime Clock" version (V3). It actually works.

"I'm not crazy. This is real."

A brief explanation of the chart below: V2 are the Prime Wheel results and V3 is the for Prime Clock. "Fail Reasons" refers to Composites that are produced and the number on the left is the lowest Prime Number that makes up the composite. The Number to the right of the Prime is how many times that happened (7 was the smallest Prime factor of a Composite 3,808 times). So for counting numbers 1 to 100,000 about 17% are Composites as produced by a 30-slice wheel. The Prime Clock produces 0.0%.

Above 100,000 the Prime Clock continues to produce all of the Prime Numbers and none of the Composities. It's producing every single prime number so the results are not instant. But it's faster than handing the overhead of Trail Division required by a simple Prime Wheel:

My application lets you set a range for the calculations, so you don't always start with 1 and work your way up. In the test above I chose three starts at a Million, a Billion, and a Trillion. I also only generated Primes for 100,000 numbers at each level so the timing would be more about calculating and less about writing out a ton of numbers.

If you look at the time increase from a Billion to a Trillion, you can see the Wheel performance time goes from a minute twenty three seconds to over seven hours. Something exponential seems to be revealed there. The Prime Clock produces the same result in a little over four minutes. Huge improvement!

I'm not totally sure if one result is exponential and the other is some form of linear. The number realm has increased 1,000 times (billion to trillion) and neither method is 1,000 times slower. On the other hand the requested Prime range is the same 100,000 for both and in the "world of string manipulation" (like arithmetic) the time it take would be almost the same at any scale.

There is linearity with increasing the Prime Set range from 100,000 to 200,000 to 400,000 in the Trillion realm. As the number set being requested doubles in size, the time it takes is actually a bit less than double. This indicates some shared overhead, but a linear response to the workload. Moving the realm to 10 Trillion then 100 Trillion and then a Quadrillion slows the response a bit less than 10x for each 10x jump.

Breaking Bad

The Doomsday Scenario with Prime Numbers only happens if the discovery can break RSA Encryption. Breaking would be bad. In "The Numbers" I mention the RSA Factoring Challenge that started with a softball 10¹⁰⁰ Composite. The Challenge was to find the two primes that when multiplied together equal this "RSA-100" number. As a headstart they let you know both prime numbers are 10⁵⁰ and if you find one you arithmetically have the other (by division). To verify a 10⁵⁰ Prime Number you need to make sure it isn't divisible by any prime up to 10²⁵. Since we are looking for a simple benchmark let's make it even easier and generate all the Prime Numbers up to 10²⁴.

To generate primes to a Quadrillion (10¹⁵) I needed to previously generate files of primes from 1 to 32 million. I chose a reasonable method, which was each file was named for the max candidate (e.g. 32_million.txt ) and each file would cover 10⁶ of the number range. These files are only about 500K in size and take about 30 seconds each to create. From experience I know 1,000 files in a folder is a happy upper limit, so the file standard for all these Primes would be a range of 1 million for each file, with a thousand files in each folder. So 10⁶⁺³ or 10⁹ covered in a single folder. Seems like we are on our way!

Once we fill a folder, it needs to nest into another folder, creating a hierarchy of the prime containing files. This convention also allows us to quickly navigate to the specific file containing any prime. Each higher level folder contains 1,000 folders in it. So how many folder levels will this require?

• 10⁶  — Each file with range of one million
• 10⁹  — Folder Level 1
• 10¹² — Folder Level 2
• 10¹⁵ — Folder Level 3
• 10¹⁸ — Folder Level 4
• 10²¹ — Folder Level 5
• 10²⁴ — Folder Level 6

6 folder levels deep? This is sounding reasonable. The file size at 500K seems fine too. The number of digits for each prime number will grow as the range grows higher, but there will be fewer primes per file. So space doesn't seem to be the constraint. How about time? Running an unoptimized program on an old computer currently takes about 30 seconds per file. Let's imagine a programming/technology gain that reduces that time to 1 second for each million candidate file. How long to generate the full set? A long lunch? Overnight? A full weekend?

We can assume the folder creation part of the workload is negligible. It's all about creating each file at 1 second each. How many files need to be written? Since each file already contains 10⁶ and we are covering 10²⁴ we only need 10¹⁸ files. How long would that take?

A clue comes from "Speed of Life" where the range of bacterial movement to the speed of light is captured within 10¹². And the electromagnetic spectrum, from kilometer length radio waves down so gamma waves narrower than the nucleus of an atom, is captured by 10¹⁵. So what is 10¹⁸ seconds?

10¹⁸ Seconds is over 31 Billion Years!

Scientific notation is how we get tricked into assuming there might be reasonable solutions for unreasonable numbers.

GPT-4 is an example of success coming from throwing an almost unreasonable amount of resources at a problem. Training GPT4 supposedly took a farm of 25,000 dedicated GPUs, 100 days, consuming $100 million. What if we used that level of horsepower for the Prime Clock?

Without getting into too many tech details, let's assume each hardware unit is 100x faster than our benchmark "one-second machine." So each faster unit can produce a completed file in 1/100th of a second. Instead of 25,000 units, lets go for 100,000 units (4x ChatGPT). So now the throughput would be 100 x 100,000 faster (10⁷) leaving 10¹¹ seconds, or a still bit over 3,000 years to process everything. Of course at Cloud pricing of $4 million a day (based on the GPT4 numbers) that would be WAY TOO EXPENSIVE, and take WAY TOO LONG.

100,000 NVIDIA A100 GPUs is what Microsoft is estimated to need for its future Bing model. Let's go crazy and say we want 1,000 times more units than even Microsoft will have (so a 100 million unit farm). I'm not sure about cost or even available electricity, but it reduces the time down to 3 years. Happy?

After we've used up all of the money and all of the electricity on the planet brute forcing RSA-100 down to 10⁸ seconds (3 years), the nice folks at RSA just increase to RSA-110, and we are right back to 10¹⁸ seconds (31 billion years).

A single RSA-110 number was factored as part of a contest using a very different methodology than producing ALL of the primes. In fact, RSA-250 is the largest challenge solved (after the contest ended, so no prize!) and it took 2,700 CPU core-years of distributed computing and guessing to find that single number (not the whole range). RSA even had a 617 decimal digit challenge but no one ever got close.

Safe!

RSA Encryption is safe. It's safe from the Prime Clock, which means we are safe too. We are safe as members of an encryption dependent society and we are safe as knowers of the secret.

I was discussing paradigm shifts with a friend and he stated "It's like you wanted to build something to fly, but were an expert at bicycles. No matter how much you improve the bicycle, it's not going to fly. You have to start over."

The Prime numbers seem like a cosmic challenge. People on the ground think the prime numbers are random, but the Prime Wheel actually allows us to fly. The Prime Clock does the seemingly impossible, breaking free of the atmosphere and putting us into orbit. Space flight!

But then the goal moves and now we need to get to Vega ("Contact" reference) to confirm extraterrestrial intelligence. And Vega is still another 4 light years away and not something we can come close to doing with this new "space bicycle."

If the Prime Clock is real, and yet doesn't break encryption, what is is really doing? That will be the topic of the final article in this series, "Philosopher Stones."

---

HOME »

The other articles in Boundaries of Objectivity will explore this further. You can leave thoughtful comments or questions at the link below.

Comments   ?