Previously on ARCHIE...

In Part One I introduced the ARC Prize Challenge.

My primary focus has been to contrast the "Orthogonal" philosophy ARCHIE takes to Big Tech's reliance on massive data and computer power. The compact design of ARCHIE requires Curriculum learning versus Supervised or Unsupervised training. This drives software decisions to favor transparency and human interaction over maximum code efficiency. ARCHIE is intentionally not a "Black Box" and produces entirely deterministic and repeatable results.

On page 26 of "On the Measure of Intelligence" François Chollet identifies "four broad categories of innate assumptions that form the foundations of human cognition:"

• Objectness and elementary physics: humans assume that their environment should be parsed into “objects” characterized by principles of cohesion (objects move as continuous, connected, bounded wholes), persistence (objects do not suddenly cease to exist and do not suddenly materialize), and contact (objects do not act at a distance and cannot interpenetrate).
• Agentness and goal-directedness: humans assume that, while some objects in their environment are inanimate, some other objects are “agents”, possessing intentions of their own, acting so as to achieve goals (e.g. if we witness an object A following another moving object B, we may infer that A is pursuing B and that B is fleeing A), and showing efficiency in their goal-directed actions. We expect that these agents may act contingently and reciprocally.
• Natural numbers and elementary arithmetic: humans possess innate, abstract number representations for small numbers, which can be applied to entities observed through any sensory modality. These number representations may be added or subtracted and may be compared to each other, or sorted.
• Elementary geometry and topology: this core knowledge system captures notions of distance, orientation, and in/out relationships for objects in our environment and for ourselves. It underlies humans’ innate facility for orienting themselves with respect to their surroundings and navigating 2D and 3D environments.

We should keep all of these in mind as we explore the inner workings of ARCHIE to see if it matches these criteria.

How does ARCHIE Solve the ARC Puzzles?

The ARC Prize has a Discord site where members text about ways they are trying to solve the challenge. The first thing I remember was a student trying to get help with dumping JSON files straight into an LLM so it would find associations between documents and consequently solve the puzzles. This is NOT a method ARCHIE utilizes.

ARCHIE tackles ARC as sets of visually-represented, abstract problems. It moves beyond formatted JSON and numerical values as quickly as possible.

As mentioned in Part One, the ARC Puzzles are presented in a JSON format. JSON stands for JavaScript Object Notation and makes sense for structuring data on a web page which renders the data via a JavaScript program. For ARCHIE, I read the native JSON and convert it to values in rows and columns (like a spreadsheet) that is very human-readable. Once loaded, the program does not need to refer back to the JSON file.

From here on I am going to refer to the colored squares as "pixels" even though in the application they are button objects. A pixel has 3 values: the row, the column, and the color. The color is represented by a digit from 0 to 9.

I arranged ARCHIE's palette so it's easy to convert a number to a color by observation:
0=Black, 1=Blue, 2=Red, 3=Green 4=Yellow
5=Grey, 6=Fuchsia, 7=Orange, 8=Teal, 9=Brown

Objectness and the Figure-Ground

ARCHIE's very first task is to detect the Objects in each of the Input grids. An Object in this context (which should match Human perception) is a group of touching pixels, which are usually the same color and are not the Background. "MultiColor" Objects are one of several "paradigm variants" ARCHIE handles (but we will save that discussion for later). The paradigm we will focus on is the "Object against a Background" paradigm which most of the ARC puzzles fall under.

A simplistic analysis is that all the Black pixels are "Background." That's the case for the current puzzle and most others, but Teal is another popular Background. ARCHIE does an analysis of the specific puzzle Background before attempting to detect any of the grid Objects.

Human vision processes all of the grid "Pixels" simultaneously. The sensory input moves up a hierarchy of neurons (real ones) that assemble in the brain, detecting an object. The challenge for a computer is that only a sequential scan is available, one pixel at a time, left to right; top to bottom (and then a reverse scan). As a scan proceeds through each column of each row, 8 neighboring pixels have to be evaluated for contiguity. The pattern looks like this:

After the pixel groups are arranged into Objects, they are named and noted in a field:

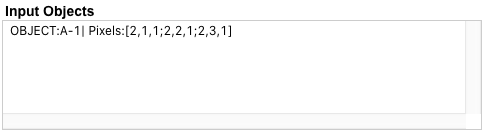
We have identified the one object in this grid and uniquely named it OBJECT:A-1, designating it the first object in Example 1. The three Pixels that make up the Object are noted, and Background Pixels are ignored. We are now ready to gather Attributes for this Object:

This analysis pass has picked up Attributes (amount and color of pixels, height and width of the Object, etc.) and modified the record on this Input Object line. One more pass compares this Object to other Objects in the same Input grid. This is where the relative and normative attributes are recorded, such as "rSize:1" and "nSize:Largest." (Relative Attributes don't really come into play with single Object Grids, but are crucial when Multiple Objects are involved.)

We are now ready to inspect the Output Grid and see what type of transformations have occurred.

The analysis of the Output Grid begins by checking on the status of the Objects detected in the Input Grid. These Objects can be [Static] = unchanged in any way, [Modified] = same pixel positions but with one or more color changes, [Partial] = some pixels are missing and are replaced by Background pixels, or [DELETE] = all the Pixels from the Input Grid for this Object are now missing.

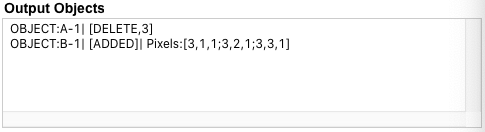
OBJECT:B1 is formed by the new Blue pixels in the bottom row of the Output grid. It's [ADDED]. These pixels were not part of the Input Grid. Following the Core Fundamental of Persistance: Objects do not suddenly cease to exist and do not suddenly materialize. ARCHIE needs to account for an Action initiated by OBJECT:A-1 which caused both the observed [DELETE] and new [ADDED]. In fact, ARCHIE will not submit an answer if any [ADDED] Records remain in the Output Objects list.

ARCHIE uses a process of elimination to determine the most likely Action, which in this case is [MOVE]. This Action functions as both an explanation and a proposed Command. These Commands function as mini-programs much like Spreadsheet Formulas. [MOVE,r0,1,0] has 3 parameters: r0,1,0 which are interpreted: r0 = rotate the Object 0 degrees (supporting other rotations or Object flips); 1 = Add one to the row position of every pixel in the Object; and 0 = Add zero to the column value of every pixel in the Object. To extend the functionality of the [MOVE] command, ARCHIE can substitute the row and column constants with Object relative variables like 'pHeight' or 'pWidth'. In this way, ARCHIE creates a set of compact and powerful mini-programs to be later used when transforming Test Objects.

Progressive Theories of the Human Problem Solver

Right now we have seen the direct solution for a single input/output example, and the resulting Command, but there is no evidence of Abstract Reasoning yet. We need to work through the entire puzzle to evaluate that:

Right now as a human problem solver, I see 2 Blue objects that move to the bottom. So that's the current Theory for this puzzle.

When we take into account the third example pair:

The third pair confirms for us: "Yes they are Blue, and they all have 3 pixels, BUT instead of moving to "the Bottom," these 3-pixel blue objects are moved DOWN one row." This is as good a characterization of the examples as any. So how do we transform the Test Input Object to produce the single correct answer?

Countervailing Evidence and Consensus

To Solve the Test Input Grid now requires Abstract Thinking, or at least a
Process of Generalization.

The Test Input Object is not 3 pixels and it's not even Blue! As a Human, I must say "Oh well" and toss out some preconceived notions about the rules of this transformation. If I get rid of the parts that cannot be applied (Color:Blue, and pCount:3) then I am just left with moving the only Object present down one row. But how could a "hard-coded" program like ARCHIE solve this?

The Key is Comparing Actions, Objects, and Attributes

The next level in ARCHIE's problem-solving Hierarchy is named "Compare." What it does is assemble all of the Actions identified in the examples (above) and then look back to the Input Objects to match their Attributes:

Compare Output Objects

When ARCHIE removes the inconsistent Object Attributes (pHeight and pWidth) we are still left with pCount:3 and Color:Blue. So that would not provide any solution since the Test Object is Color:Red and pCount:2!

But there is one last level in the Abstraction Process: Theory.

The Theory Process evaluates what is common from the Compare Process, and then matches it against the Attributes of the Object in the Test Input grid. The final pronouncement is what is in common across the board.

The Final Process is to apply the Actions from Theory methodically to each Object in the Input grid.

Results render to the screen –

The red 2-pixel Input Object has dropped down one row and...

Summary of Progress

• ARCHIE quickly moves from the source representation of an ARC Puzzle to list the Input Objects against a Background. Moving forward it works with listed Objects instead of directly with numbers in a grid.
• Input Objects are compared to Objects in the Output grid, resulting in a "Static," "Modified," "Partial," "Delete," or "Added" status.
• Following the principle of Persistence, Actions are assigned to Objects in order to account for the state change of the output grid.
• Actions assigned to Input Objects are matched to the calculated Attributes of those Objects.
• Actions with Attributes are compared across all Examples. Only the Attributes common to all Examples are retained.
• A "Theory" stage assembles Actions that could be applied to Objects in the Test Input Grid.
• The final "Action" stage applies these consolidated Actions to the Test Objects and renders the final Solution Grid.

What's Next?

PART THREE will describe more difficult examples and reveal more about ARCHIES's abstraction capabilities.

PART THREE»