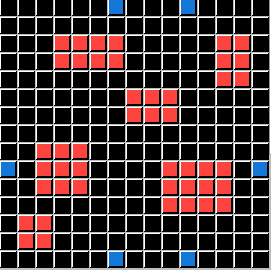
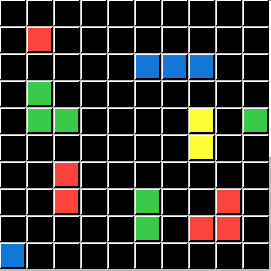
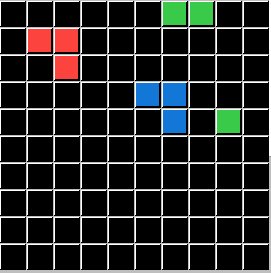
This puzzle represents the Logic condition pΛq. In this series of custom puzzles P represents the Color Green and Q represents a Pixel Count of 3. So DELETE Objects that are Green and have a total pf 3 Pixels:
⇨ ? 
ARCHIE Part Six
An Orthogonal Approach to Artificial Intelligence
Darren Lott
February, 2025
February, 2025
Previously on ARCHIE...
In Part One I introduced the ARC Prize Challenge.
In Part Two We analyzed a simple Puzzle requiring the Action MOVE.
In Part Three We introduced the PAINT Action and the IF-THEN-ELSE conditional.
In Part Four We introduced the STROKE Action and Objects that are partially revealed.
In Part Five We introduced the EXTEND Action and Utilizing Compound Actions.
⇨ ?
ARCHIE: Intuitive Logician
Understanding Symbolic Logic is not part of ARCHIE's codebase nor was it part of the Curriculum.
This was an UNEXPECTED Capability!
Recalling IF-THEN-ELSE
⇨ ?
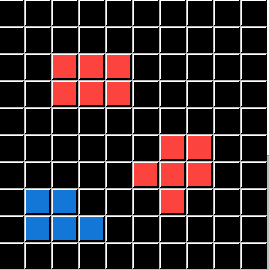
The order of applying ACTION Rules to Test Objects was part of my own metacognition concerning the ARC Puzzles. How would I solve this? Part Three shows a puzzle that first gave me a clue that ARCHIE had already picked up a Conditional Statement without any explicit coding or even anticipated functionality.
If ARCHIE already handled IF-THEN-ELSE, what other parts of Logic did the Architecture capture?
Quintessential Symbolic Logic Statements
There are 5 canonical conditionals in symbolic logic:
- pΛq – BOTH p AND q
- p⋁q – p OR q
- p⊻q – p OR q BUT not BOTH
- p->q – IF p THEN q
- p<->q – p IF AND ONLY IF q
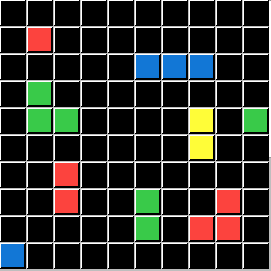
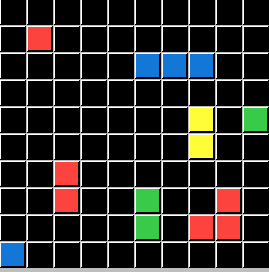
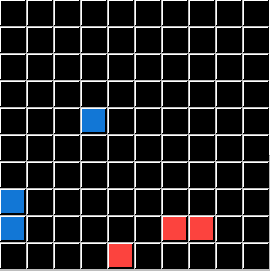
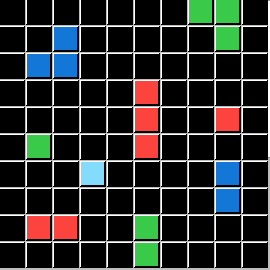
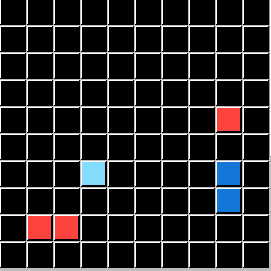
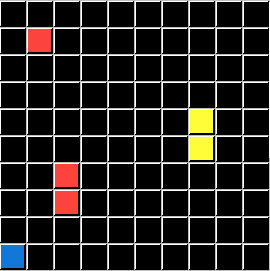
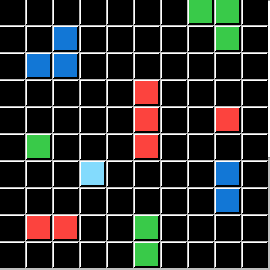
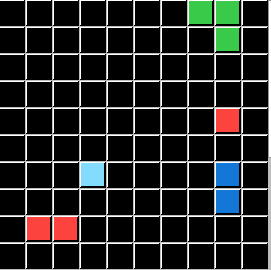
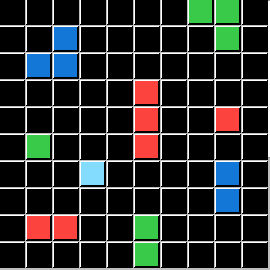
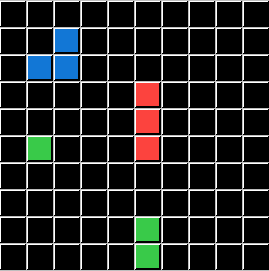
I will demonstrate these conditions using the same Input Grids and the same Test Grid for all five. Only the Output Grids will change for each demonstration, directly illustrating a Logic State that ARCHIE (and you) are challenged to solve. To save you time and effort I will now reveal that P is always the Color Green, and Q is always the Pixel Count of 3. The ACTION is always DELETE. All that is left is for you to apply the correct Logical Statement. (ARCHIE didn't get or need those hints.)
Demonstration 1
⇨ ? 
⇨ ?
Demonstration 2
⇨ ? 
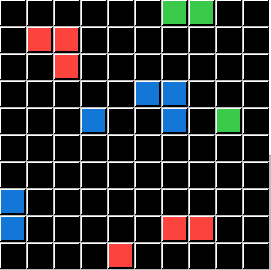
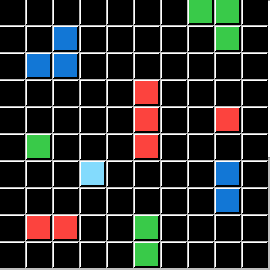
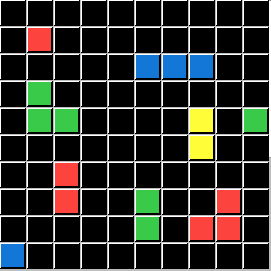
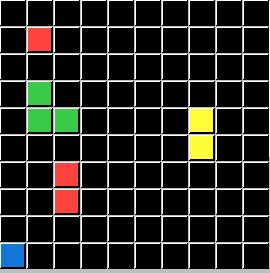
This puzzle represents the Logic condition p⋁q. This the Logical OR. So DELETE Objects that are Green OR have a total of 3 Pixels:
⇨ ? 
Demonstration 3
⇨ ? 
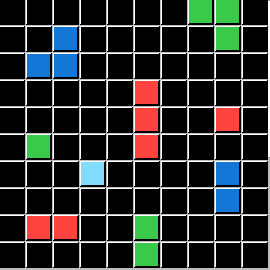
This puzzle represents the Logic condition p⊻q. This is Logic's EXCLUSIVE OR. It's trickier as you must DELETE Objects that are Green OR have a total of 3 Pixels, BUT leave as Static OBJECTS that are Both Green AND have 3 Pixels. This is the most interesting conditional for ARCHIE because it shows how "Static" can function as both a benign OBJECT Status and also as it's own ACTION, protecting an OBJECT against other further ACTIONs (like DELETE).
⇨ ? 
Demonstration 4
⇨ ? 
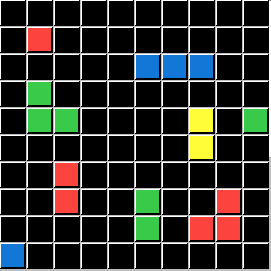
This puzzle represents p->q. This is an IF THEN statement.
People new to symbolic logic will find this conditional has obvious and also not-so-obvious sides. To judge when "IF P THEN Q" is true, you intuit that a state of (P = True) and (Q = True) is obviously True. Where (P = True) and (Q = False) is obviously False - the promise has been broken. Less Obvious are the two other states:
(P = False) and (Q = False) is also TRUE.
(P = False) and (Q = True) is also TRUE.
For p->q, when P is FALSE Q can be either. It's an interesting statement with 3 ways out of 4 to be TRUE.
⇨ ? 
Demonstration 5
⇨ ? 
This puzzle represents p<->q. This is the IF AND ONLY IF statement. Another quick way to inspect the solution to this and the other Demonstration puzzles is checking which OBJECTS didn't get deleted. Who survives?
Here we are left with Green Objects unless they have 3 pixels. And if they are not Green, they remain Only IF they do have 3 pixels (the remaining Red and Blue Objects).
⇨ ? 
Review of ARCHIE's Abstract Reasoning Abilities
- ARCHIE has perfect access to mathematical abilities where required.
- ARCHIE uses elementary arithmetic sparingly when analyzing and executing ACTION Rules.
- Attributes assigned to Objects can be Cardinal (1,2,3), Ordinal (first, second, third), or Normative (Tallest, Smallest).
- ARCHIE classifies orientation in terms of 8 compass directions (N,NE,E,SE,S,SW,W,NW).
- ARCHIE classifies distance in terms of integers (3 rows down, 2 across), Border Crossing, Object Collisions, and Relative Attributes.
- ARCHIE accesses Functions pertaining to an OBJECT's Abstract Properties (e.g. the Body, Sides, and Corners of a rectangle).
- ARCHIE innately detects and executes any logical condition.
- ARCHIE solves problems in a deterministic, hierarchical fashion.
Wrapping Up!
CONCLUSION will review ARCHIE's current capabilities and propose future advancements.