In 1962 Proctor & Gamble created an advertising campaign, offering a $10,000 prize to whomever submitted the shortest route linking 33 defined US cities. That prize was enough to buy a house at the time. And I missed it.

Finding the shortest route between a set of locations is a class of mathematical problem known as "The Traveling Salesman Problem" or TSP. It is an optimization problem, easily solved when the number of locations is very small, and seemingly impossible with larger sets. In fact, anyone who engineers the "definitive algorithm" for this problem will have solved the P=NP challenge by the Clay Mathematics Institute, and be awarded $1,000,000. Show me the money.

Myths are but Congealed Memories

In my fanciful recollection, guys at the Rand Corporation won the contest by placing push pins into a US map and then by stringing a loop of yarn around the perimeter. The shortest string provides the solution to the shortest distance. It's a bit of analog genius!

Unfortunately, my recollection is slightly apocryphal. In Pursuit of the Traveling Salesman by William J. Cook provides a comprehensive account of the TSP and its history. The Rand gentlemen did use a peg and string method to get started, but eventually performed Linear Programming by hand to solve the shortest 49-city tour, in 1954. They did not win the 1962 P&G 33 city contest. That ended in a tie between two mathematicians, who then had to write an essay on the virtues of P&G soap as the tiebreaker.

Of Course, I Built an App

To be honest I didn't know about the P&G contest or the Clay Institute when I got started exploring TSP. I read some Computer Science grad students made a minuscule improvement over existing methods and I wanted to see if I could do better. I built my "TSP Explorer" as an interactive application to try some of the known approaches and see if I could dream up any improvements.

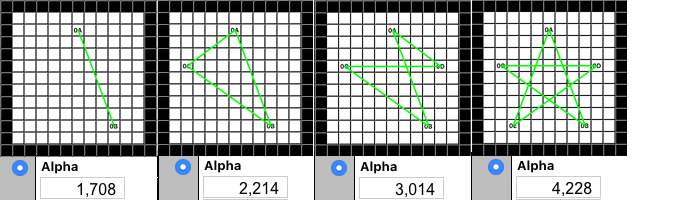
The first step was to build a grid and a way to populate locations. My grid was an array of square buttons that toggle and label themselves in alphabetic order.

The second step was auto-connecting each location (green line) as it is populated in alphabetical order and calculating the total distance. You can see this above as the Star is being formed and the total Alpha distance is finally calculated at 4,228, which is the pixel distance from the center of each button to the next. A feature of TSP is that each location must be visited in a specific order, and that sequence is called the "Tour." The last location always links back to the starting location, and that distance also counts.

Optimization Algorithms

It's amusing to click around, create shapes, and note the distance. But the real work comes with improving the Alpha distance to get a shorter path. Brute Force is the Gold Standard for finding the shortest distance. But it becomes an unusable technique with a shockingly small number of locations.

From this article's banner image, you can tell that 33 locations result in too many permutations to check. Fortunately, the 5 locations in the "Star" example above are no problem and seem instant. 8 locations take about a few seconds but 9 locations escalate to a minute. I put in a check to prevent attempts over 10. More efficient code and a faster computer would allow a few more locations to be Brute Forced, but not many more.

Spiral Locations Comparison

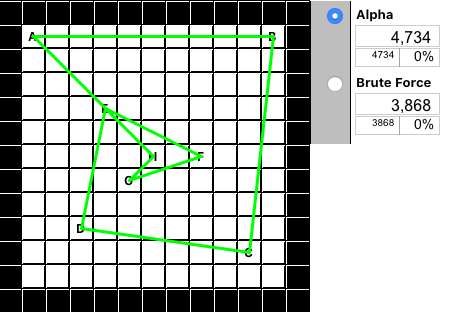
To compare Brute Force to the other algorithms we are about to encounter I made the quick spiral pattern above and ran Brute Force against it. We now know that no path shorter than 3,868 will be found. Because we exhaustively checked every possibility.

Alpha Algorithm

The Alpha algorithm routes through each location in the order they were entered. Since each new point gets a later letter designation this also happens to be in alphabetical order. The distance can be pretty long for tours entered randomly, but an imported, optimal tour might result in Alpha being the shortest distance (at least for a while!). The Alpha tour distance above is far from optimal at 4,734.

Brute Force Algorithm

The number of permutations required to Brute Force a tour is (n-1)!/2. You can read more about this type of notation in my article "Comprisation." But if we take 8 locations like above, the calculation is (7*6*5*4*3*2)/2 = 5040/2, or 2,520 full tour distances. If that doesn't seem like very many, remember that for every set of points, the unique distance between them has to be calculated and then added to the overall distance of that tour. And then all the tours need to be compared to find the shortest one. (The reason the formula is not just 8! is because, with the circular nature of a tour, the finished sequence is independent of a start. And the circular distance is the same, forward or backward. But if you are Brute Forcing a segment of a tour then the formula is the full n!) Again, the shortest tour distance is now known to be 3,868.

Greedy/ Repetitive Nearest Neighbor

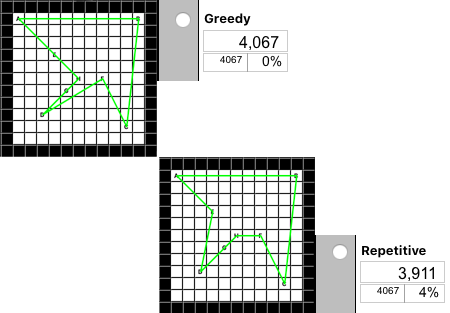
A very simple algorithm to find a short tour is the "Greedy" technique of "Nearest Neighbor." To execute this you pick the first location (A) and then check the distances to all of the remaining locations. Pick the closest one (E), add it to the tour, and then find the next closest remaining location (H). This is a fast and fairly productive method. Unless the last remaining location ends up pretty far from the start, which seems to happen frequently. Since the success of "Nearest Neighbor (NN)" is highly dependent on the starting location, a more optimal algorithm is "Repetitive Nearest Neighbor (RNN)." This runs the individual NN algorithm, trying each of the possible locations as the starting point, and notes the total distance for that tour. It finishes by comparing the distances of all the tours and picks the shortest. It takes as many times longer to execute as the simple NN as there are locations (8 times longer in this example), but it always produces equal or better results than Greedy. In this example, the optimal RNN starts at (F) and the tour is 3,911. Much better than Alpha, 4% better then the single pass "Greedy" approach, but still longer than the Brute Force optimum.

Near Inserts Algorithm

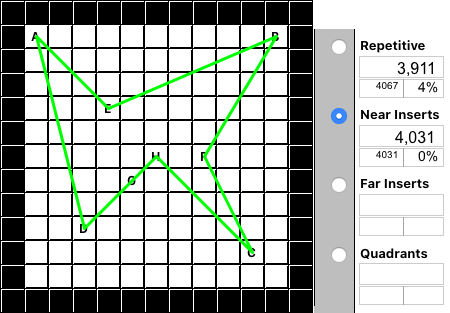
"Near Inserts," in my experience, produces the most variable results compared to the other algorithms. Sometimes it's good, sometimes not. It starts by checking ALL of the locations and it picks the closest pair and connects them (H-G). Then it finds the next closest to any of those and inserts it (F-H-G) and so on (E-F-H-G), (D-E-F-H-G)... The theoretical advantage of this approach is whenever the next closest location is found, it's not added to the end of the chain, like with "Nearest Neighbor", but rather it's inserted at the closest point in the middle (D-A-E-F-H-G). If you watch the tour being built, it's similar to a balloon being blown up from the center until it reaches all locations. In this example it slightly outperforms the single pass NN, but not the Repetitive NN.

Far Inserts Algorithm

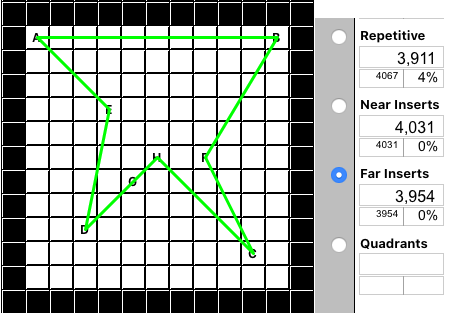
Watching "Far Inserts" proceed seems like shrink wrap is placed around the outer perimeter of the location groups, and then incrementally collapses down to join the inner locations. It also inserts into the building tour, contrasted with only adding to the end. "Far Inserts" usually outperforms "Near Inserts". Frequently, it produces the result closest to optimal. But in this example, RNN still created a shorter tour, and neither matched the "Brute Force" optimum.

Quadrants Algorithm

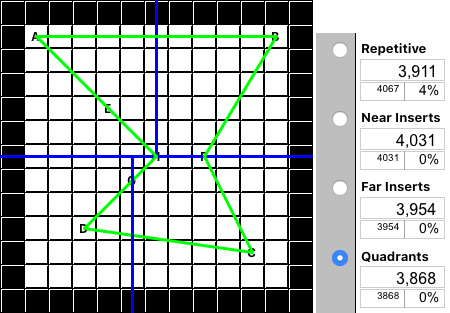
The previous algorithms are standard methods for solving a TSP tour. (Note the different approaches all resulted in different suggested tours.) "Quadrants," on the other hand, is my own totally unique approach. It's also the only algorithm (in this example) that found the same optimal solution as Brute Force! (3,868).

I have to admit a bit of serendipity as I designed "Quadrants" for larger problems, where there are too many locations to Brute Force the solution. What I was looking for was a way to be sure about optimal sub-sections of a longer tour. That approach suggested brute forcing smaller segments and then joining them together.

Another thought behind the "Quadrants" algorithm was the observation that most completed tours form a sort of circle or polygon-type shape. Optimal solutions don't cross back and forth, nor do they have open ends, or form snake or U shapes. I started applying a quadrant graph overlay of examples of various optimal solutions and noticed the good tours entered and exited a quadrant only once. By dividing the number of locations into 4 quadrants, I felt there was a better shot at being able to use Brute Force on larger sets of locations. (eg. Brute Force on 32 locations: NO. Brute force on 8 locations x 4: YES!)

Armed with a better tool, it's time for a larger challenge.

PART TWO »