I learned a lot from the smaller TSP location sets. In order to try the algorithms against the historic 33-City Challenge I made a larger grid and added a numeral to the letter assigned at each location. With 26 letters (A-Z) preceded by ten numerals (0-9), I could attempt challenges with up to 260 locations.

The second important enhancement was to add the ability to overlay a transparent image on the grid. With a visual diagram of someone else's challenge, I could map locations and recreate their tour without a data file.

Recreating the P&G Winning Tour

The overlay enhancement was particularly critical to the 33-City Challenge. I had, at best, an old illustration of the winning solution. There could be no data file, or any attempt to mathematically convert it to my grid coordinate system. But by clicking buttons, in order, under each of the image locations, the "Alpha Algorithm" theoretically captures the historic "Optimum Solution."

There are way too many locations to use "Brute Force" and since "Repetitive NN" matches or beats "Greedy" we will drop showing those algorithms for brevity. You will also notice that the red dots from the historic illustration don't always map perfectly over the center of the grid squares. The Alpha solution tour is calculated above at 10,709 units, which represents the pixel distance from the center of each activated grid object. When the Rand team researched the optimal tour of 49 US locations (48 states plus Washington DC) they came up with 12,345 miles. Cutting their locations from 49 to the Contest's 33 locations, the 10,709 Alpha distance might be a pretty good stand-in for miles too.

A Challenger Appears

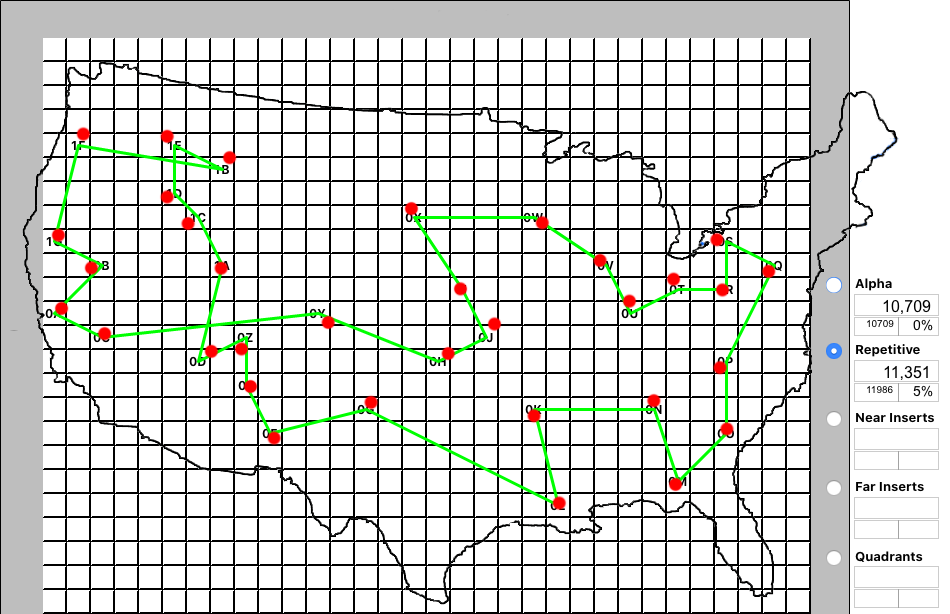
The "Repetitive Nearest Neighbor" gets a shot and doesn't do too bad. Details show it is a 5% improvement over its initial "Greedy" attempt. At 11,351 it's still about 6% longer than the Alpha tour. But notice the tour path crosses over itself twice in the Western part of the map. That indicates an optimization technique can be run against this tour, removing the crossovers and shortening the distance. Will it be enough?

Not Nearly Good Enough

The "Near Inserts" Algorithm doesn't have any crossovers, and yet still falls short of the mark. At 12,524 it's about 17% longer than the Alpha tour. Just eyeballing the solution suggests something is problematic over Arizona.

Far Inserts is Far Out!

The "Far Inserts" tour just looks like a more optimal solution. There are no crossovers and no pinch points. At a distance of 10,441, it actually is more optimal! "Far Inserts" is 2% BETTER than what we previously benchmarked with the Alpha tour. How can this be? First, we don't know for sure if the historic P&G solution actually was optimal. Second, the slight misalignment of locations on the grid might impact comparisons. Also, the historic distance between locations was supplied by a Rand McNally driving atlas. Our algorithms use straight lines between points to calculate distance. But what is of interest now is finding out if this is actually the new Optimal Tour. Can it be improved?

C'mon Quadrants...

If you run these various algorithms against many different problem sets, you end up getting attached to certain ones. Certainly, I find myself rooting for Quadrants since it's my baby. In this case, it got very close to the Alpha benchmark but fell behind Far Inserts as the best algorithm. It also has a crossover in the upper left quadrant, so perhaps running the optimizer now, to remove the crossovers, could change the finish order.

To be fair, I will rerun ALL of the algorithms again with the crossover optimizer.

Crossover Detection ON

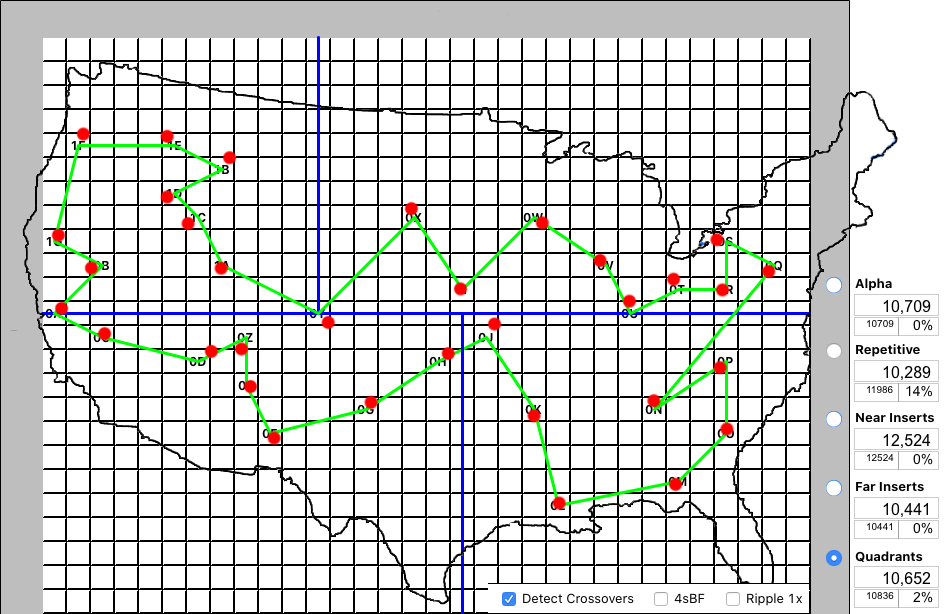
Removing the crossover in the upper left quadrant made a 2% improvement and allowed Quadrants to outperform the Alpha benchmark!

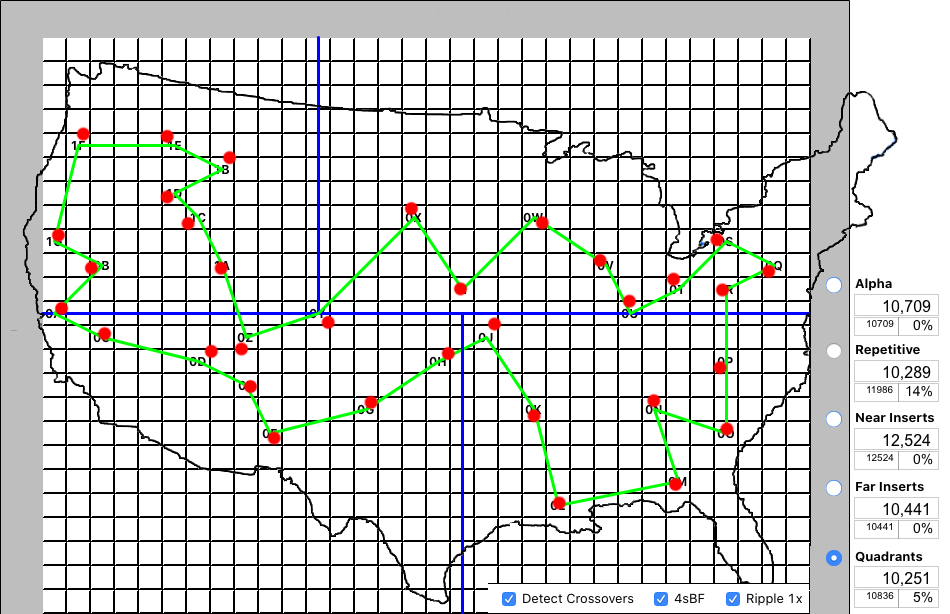
The tours without crossovers were not improved. Quadrants is still a bit behind Far Inserts, but wait. Look at the new result for Repetitive. Wow, a massive 14% improvement and a new lowest distance. One of the reasons is that I applied the crossover optimization at every pass through the Repetitive tours, and not just the last tour that had been selected as best. So a potentially great tour had been hiding amongst the various starting locations, which Repetitive just revealed.

Full Optimization ON

Removing crossovers is not my own innovation, but I had to do some research on how to implement it. I do give myself credit for applying this optimization at each level of Repetitive, instead of just at the end, and we've just seen that it pays dividends. Essentially it is a specific case of "2-Opt" where the sequence of two locations is swapped. Another optimization that is widely cited is "3-Opt." This swaps 3 locations in an attempt to shorten a tour. In my experiments, I found that 3-Opt rarely provides improvements to a good tour, and it never compares to my own optimization techniques.

4sBF

I'm going to jump ahead and apply my two favorite, and generally most effective optimizations. "4sBF" runs through a completed tour and takes 4 location sub-sequences and then applies a mini Brute Force (BF) solution to those four. The theory is that regardless of how long a completed tour is if you can snip out a sub-segment, shorten it, and splice it back in, the overall length should now be shorter. To be even more complete, you cycle through every location and its 3 neighbors and note if the overall tour ever gets shorter. Since shortening one segment might present new possibilities, you continue full cycles until there are no more improvements. "6sBF" takes considerably longer to run (720 permutations at each location versus 24) and I usually don't activate it unless I think there might be more optimization available within a specific tour.

Ripple 1x

"Ripple 1x" is the second type of custom optimization I created. Since 4sBF is already running mini Brute Force optimizations in a circular fashion, are there any other options? Yes! Ripple.

I came up with Ripple by looking at sub-optimal tours and noticing that the locations that needed to be connected were often farther apart than any Brute Force sub-section could handle. So instead of snipping out a small sub-section of the tour, optimizing it, and reinserting it, Ripple takes out a sub-section, that keeps growing outward (like ripples in a pond) and attempts to optimize the outer sections instead. I also learned from experience that a combination of 4sBF followed by a Ripple provides better results than either method alone. Let's give it a try on Quadrants.

Ladies and Gentlemen, We Have a Winner!

At 10,251 the optimized Quadrants tour beats the Alpha benchmark, the Far Inserts leader, and even the massive improvement of the Repetitive algorithm. Visually, it looks great and it's also the best we are going to see. How can we tell? Consensus.

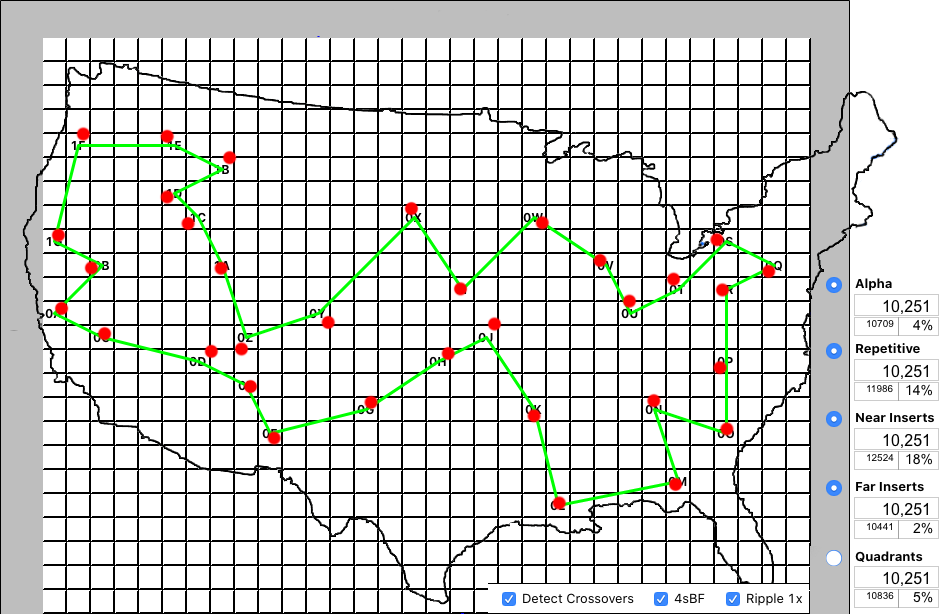
Despite using different initial algorithms with substantially different tour solutions, the application of the two optimization techniques results in the same optimal solution for the initial algorithms. Even the Alpha benchmark gains a 4% improvement.

Conclusion

Despite great results, I don't think the Clay Institute will be sending me a check anytime soon. They are looking for a definitive, one-shot, mathematical formula, applicable to any number of locations. The TSP seems to respond best to an iterative consensus approach. But I am both surprised and pleased at how well the combination of Crossover detection, 4sBF, and Ripple 1x optimizations works. I've had amazing success even when an initial tour starts as a random assignment.

When designing an artificial Neural Network you will find I selected "Repetitive Nearest Neighbor" as the optimization method. It provides impressive results even when extended beyond circular tours. You can read more about it in Black Boxes.

Ultimately, I learned a lot. These new techniques would be useful to improve on Delivery Routing or Warehouse Picking. All practical benefits, and I didn't have to declare my love for P&G's Old Spice soap.

HOME »

You can leave thoughtful comments or questions at the link below.

Comments   ?